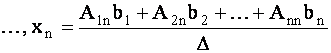Пусть задана система линейных уравнений, содержащая одинаковое число уравнений и неизвестных

(1.19)

Введем три матрицы

Матрица , составленная из коэффициентов системы, является квадратной матрицей порядка . Матрицы и являются столбцовыми и составлены соответственно из неизвестных и свободных членов системы.

Так как число столбцов матрицы равно числу строк матрицы , то существует произведение , являющееся столбцовой матрицей тех же размеров, что и матрица . Тогда систему уравнений (1.19) можно записать в форме одного матричного уравнения.

(1.20)

Для определения матрицы из (1.20) допустим, что матрица имеет обратную матрицу определяемую формулой (17). Тогда, умножая обе части (1.20) слева на , получим

(1.21)

По определению обратной матрицы ,где единичная матрица порядка . Отсюда

Следовательно, уравнение (1.21) запишется в виде

(1.22)

Матричное равенство (1.22) определяет решение заданной системы уравнений в матричной форме. Для определения конкретных значений неизвестных перепишем (1.22) в виде

,

(1.23)

где определитель, соответствующий матрице ;

алгебраические дополнения элементов этой матрицы.

Перемножив матрицы в правой части (23), найдем

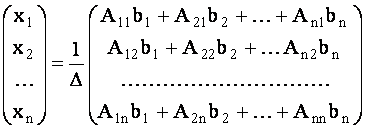
Отсюда, согласно условию равенства двух матриц, получим

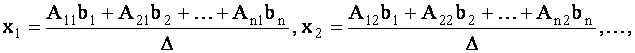
(1.24)

Формулы (1.24) и определяют матричный способ решения системы

Для запоминания этих формул и последующего их применения на практике введем группу определителей:

,

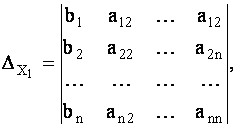
Заметим, что определитель получен из заменой его первого столбца на столбец свободных членов, определитель получен из заменой его второго столбца на столбец свободных членов и т.д.. Разложим каждый из определителей по столбцу из свободных членов Тогда

(1.25)

Из сравнения полученных результатов (1.25) с числителями равенств (1.24) следует, что решение системы (1.19) можно записать в виде

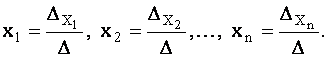(1.26)

Формулы (1.26) называются формулами Крамера.

Примеры решения по формулам Крамера

ПРИМЕР 1.1.13

Решить по формулам Крамера систему уравнений

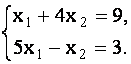
Решение. Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель этой системы.

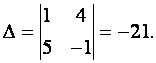
Так как ,то решение можно найти по формулам Крамера:

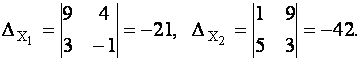Тогда

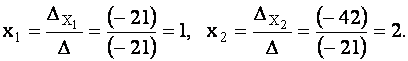Ответ: {1;2}.

ПРИМЕР 1.1.14

Решить матричным способом систему уравнений

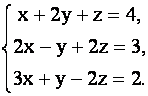
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель этой системы:

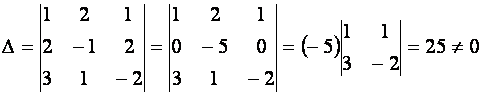
Так как , то система может быть решена матричным способом.

Составим матрицы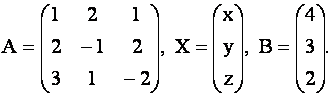

Так как определитель системы , то матрица имеет обратную матрицу , где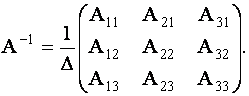

Вычислим алгебраические дополнения всех элементов

Тогда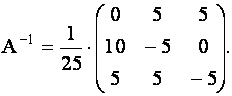

Так как решением является , то

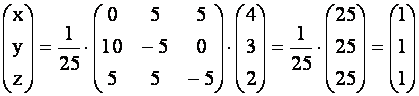
Или Ответ: {1,1,1}

• Метод Гаусса для решения систем линейных уравнений
• Курс математики