Пусть задана система из 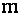 линейных уравнений с
линейных уравнений с 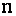 неизвестными:
неизвестными:
 |
(1.27) |
Допустим, что в системе коэффициент при 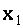 в первом уравнении
в первом уравнении 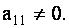 Разделив обе части этого уравнения на
Разделив обе части этого уравнения на 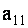 , получим равносильную данной систему:
, получим равносильную данной систему:
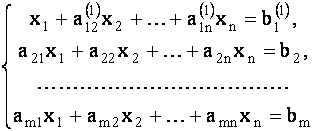 |
(1.28) |
где 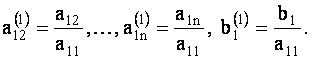
Исключим с помощью первого уравнения системы (1.28) неизвестное 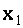 из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последовательно на
из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последовательно на 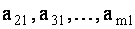 и в том же порядке вычтем полученное из второго, третьего и последующих уравнений системы (1.28). В результате получим равносильную систему вида
и в том же порядке вычтем полученное из второго, третьего и последующих уравнений системы (1.28). В результате получим равносильную систему вида
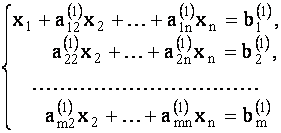 |
(1.29) |
где 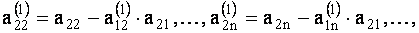
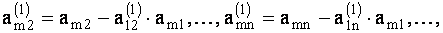
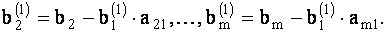
Допустим, что коэффициент 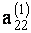 при
при 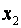 во втором уравнении системы (1.29) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.
во втором уравнении системы (1.29) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.
Исключим неизвестное 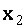 с помощью второго уравнения из всех последующих уравнений. Для этого разделам второе уравнение на
с помощью второго уравнения из всех последующих уравнений. Для этого разделам второе уравнение на 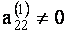 . Затем умножим последовательно полученное второе уравнение на
. Затем умножим последовательно полученное второе уравнение на 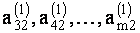 и вычтем эти результаты из третьего, четвертого и всех оставшихся уравнений.
и вычтем эти результаты из третьего, четвертого и всех оставшихся уравнений.
В итоге получим очередную систему уравнений:
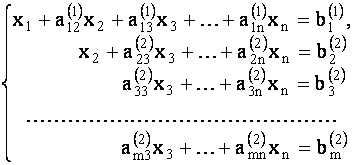
где 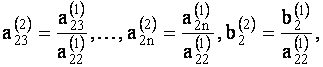
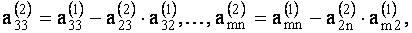
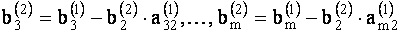
Продолжая этот процесс исключения неизвестных, получим либо несовместную, либо совместную систему уравнений. В первом случае в системе будет содержаться уравнение, в котором все коэффициенты левой части равны нулю, а свободный член отличен от нуля, т.е. уравнение вида 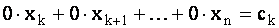 , где
, где 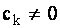 . Во втором случае получим либо систему треугольной формы
. Во втором случае получим либо систему треугольной формы 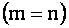
 |
(1.30) |
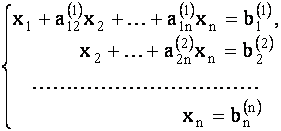
либо систему трапециевидной (ступенчатой) формы
 |
(1.31) |
В случае треугольной системы из последнего уравнения (1.30) следует, что 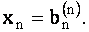 Подставляя это значение в предпоследнее уравнение системы (1.30), найдем неизвестное
Подставляя это значение в предпоследнее уравнение системы (1.30), найдем неизвестное 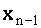 . Подставляя значения
. Подставляя значения 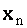 и
и 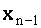 в предыдущее уравнение, найдем значение неизвестного
в предыдущее уравнение, найдем значение неизвестного 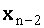 и т.д.
и т.д.
Таким образам, если данная система (1.27) с помощью элементарных преобразований приводится к системе треугольной формы, то система имеет единственное решение (т.е. система совместна и определенна).
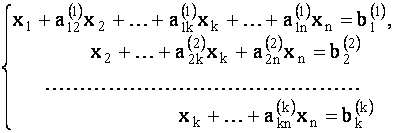
В случае системы ступенчатой формы (1.31), перенося все слагаемые, содержащие неизвестные 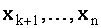 в правую часть уравнений, получим систему вида
в правую часть уравнений, получим систему вида
 |
(1.32) |
Из (1.32) следует, что значения неизвестных 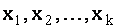 выражаются через значения неизвестных
выражаются через значения неизвестных 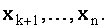 . Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.32), а вместе с ней и данная система (1.27), имеет бесконечное множество решений.
. Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.32), а вместе с ней и данная система (1.27), имеет бесконечное множество решений.
Итак, если данная система приводится к трапециевидной форме, то она имеет бесконечное множество решений (т.е. система совместна и неопределенна). Найденные решения, записанные в форме
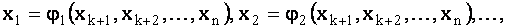
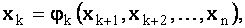 где
где 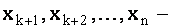 любые числа, называются общими решениями системы. Решения, полученные из общих решений при конкретных значениях свободных неизвестных
любые числа, называются общими решениями системы. Решения, полученные из общих решений при конкретных значениях свободных неизвестных 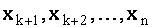 , называются частными решениями.
, называются частными решениями.
Заключение
Матричный способ решения систем линейных уравнений, как и решение методом Крамера, применим только для особых систем линейных уравнений, в которых количество неизвестных совпадает с количеством уравнений. Метод Гаусса применим для решения произвольных систем линейных уравнений и, следовательно, является универсальным методом. Этот метод позволяет существенно упростить и сам процесс поиска решений, если все промежуточные преобразования осуществить над специальной матрицей 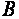 составленной из коэффициентов системы (1.27) и ее свободных членов.
составленной из коэффициентов системы (1.27) и ее свободных членов.

Матрица В называется расширенной матрицей системы. Она позволяет заменить элементарные преобразования системы уравнений на соответствующие элементарные преобразования над своими строками, что существенно сокращает процесс поиска решении.
Примеры решения методом Гаусса
ПРИМЕР 1.1.15
Решить систему уравнений методом Гаусса.

Построим расширенную матрицу системы

Исключая с помощью первой строки неизвестное 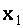 из всех оставшихся строк матрицы
из всех оставшихся строк матрицы 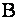 , получим
, получим
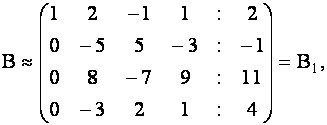
где символ 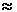 есть символ элементарного преобразования матрицы.
есть символ элементарного преобразования матрицы.
Исключая с помощью второй строки неизвестное 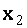 из всех последующих строк матрицы
из всех последующих строк матрицы 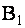 , получим
, получим
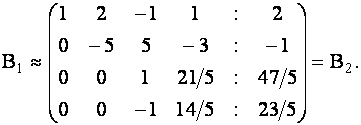
Исключая с помощью третьей строки неизвестное 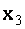 из четвертой строки, получим:
из четвертой строки, получим:
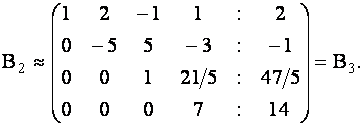
Матрица  имеет треугольную форму. Следовательно, заданная система эквивалентна системе
имеет треугольную форму. Следовательно, заданная система эквивалентна системе 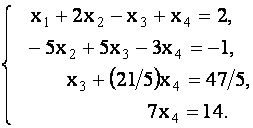
Последовательно вычисляя 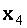 из последнего уравнения, далее
из последнего уравнения, далее 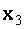 из третьего,
из третьего, 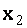 из второго и
из второго и 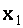 из первого уравнения этой системы найдем, что
из первого уравнения этой системы найдем, что 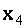 =2,
=2, 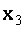 =1,
=1, 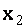 =0,
=0, 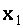 =1. Итак, заданная система имеет единственное решение
=1. Итак, заданная система имеет единственное решение 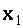 =1,
=1, 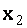 =0,
=0, 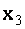 =1,
=1, 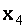 =2.
=2.
ПРИМЕР 1.1.16
Решить систему уравнений

Построим расширенную матрицу системы

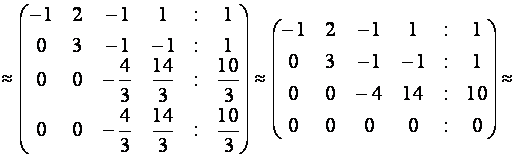
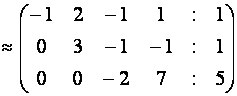
Таким образом, заданная система эквивалентна системе,
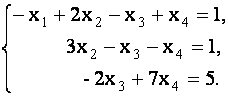
которая имеет ступенчатый вид, и, следовательно, имеет бесконечное множество решений. Выразим переменные 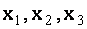 через
через 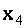 :
:
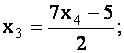
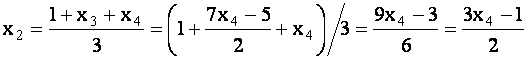 ;
;

Итак, общим решением данной системы будет
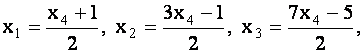
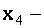 любое число.
любое число.
Полагая, в частности, 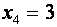 найдем, что
найдем, что 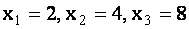 . Тогда
. Тогда 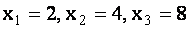 ,
, 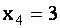 будет одним из частных решений системы.
будет одним из частных решений системы.