ОПРЕДЕЛЕНИЕ 1.29
Пусть заданы векторы 
и числа 
.
Выражение 
называется линейной комбинацией векторов . Очевидно, что линейная комбинация векторов является вектором. Рассмотрим особый случай, когда
 . |
(1.37) |
ОПРЕДЕЛЕНИЕ 1.30
Если равенство (1.37) возможно только при всех , равных нулю, то векторы называются линейно-независимыми. Если же это равенство справедливо не при всех 
, где 
, то векторы называются линейно-зависимыми.
Пусть линейно-зависимы. Тогда среди 
найдется хотя бы одно не равное нулю число. Пусть 
. Разделив обе части равенства (1.37) на 
, получим
,
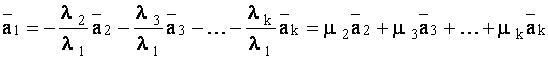где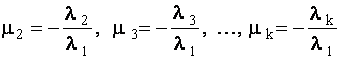 
.
Выражение 
является линейной комбинацией векторов 
. Итак, если векторы линейно-зависимы, то хотя бы один из них является линейной комбинацией остальных.
Справедливо и обратное утверждение: если хотя бы один вектор является линейной комбинацией других векторов, то вся группа векторов линейно-зависима. Пусть, например, 
.
Тогда 
и коэффициент при 
отличен от нуля. Это означает, что вектора 
линейно-зависимы.
Примерами линейно-зависимых векторов являются любые два вектора прямой; любые три вектора плоскости; любые четыре вектора пространства (рис. 1.1.12-1.1.13).
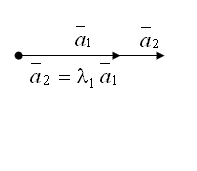
Рисунок 1.1.12
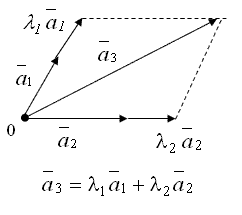
Рисунок 1.1.13
В то же время два неколлинеарных вектора и 
плоскости (рис. 1.1.13) или три некомпланарных вектора 
пространства (рис. 1.1.14) являются примерами линейно-независимых векторов.
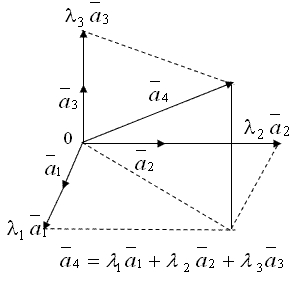
Рисунок 1.1.14
ОПРЕДЕЛЕНИЕ 1.31
Любая группа, составленная из максимального числа линейно-независимых векторов некоторого пространства 
, называется базисом этого пространства. Число векторов базиса называется размерностью пространства. Так, базисом на прямой (пространство 
) является любой ненулевой вектор этой прямой. Размерность прямой равна единице. Базисом на плоскости (пространство 
) являются любые два неколлинеарных вектора этой плоскости. Размерность плоскости равна двум. Базисом в объемном пространстве (пространство 
) являются любые три некомпланарные вектора. Размерность этого пространства равна трем.
Пусть векторы 
образуют базис 
. Тогда любой вектор 
этого пространства является линейной комбинацией базисных векторов, то есть
 . |
(1.38) |
Представление вектора 
в форме (1.38) называется разложением этого вектора по базисным векторам.
Числа 
разложения называются координатами вектора по базису . Этот факт записывается в виде 
.
Векторы 
называется компонентами вектора по базисным векторам 
.
Если векторы , образующие базис, имеют общее начало 
и вектор 
, где 
некоторая точка пространства, то числа называются также координатами этой точки. Этот факт записывают в виде 
.
