Линейными операциями над векторами называются операции сложения и вычитания векторов и умножения вектора на число.
Сложение векторов
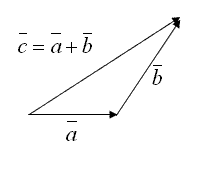
Рисунок 1.1.2
ОПРЕДЕЛЕНИЕ 1.26
Суммой векторов 
и 
называется третий вектор 
, начало которого совпадает с началом вектора , а конец – с концом вектора , при условии, что начало вектора приложено к концу вектора (рис. 1.1.2).
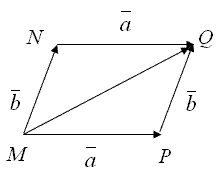
Рисунок 1.1.3
Сумма векторов может быть найдена и по правилу параллелограмма (рис. 1.1.3). Из определения суммы векторов следует, что сложение векторов подчиняется переместительному закону 
. Действительно, пусть 
, 
и 
есть параллелограмм. Тогда 
, 
и 
, 
. Отсюда, .
Понятие суммы векторов, введенное для двух векторов, можно обобщить на сумму любого конечного числа слагаемых. Например, если заданы три вектора 
и 
, то суммой этих векторов называется вектор 
, определяемый по правилу 
. Аналогично, если заданы векторы 
, где 
, то суммой этих векторов называется вектор
.
Покажем, что сложение векторов подчиняется сочетательному закону 
(рис. 1.1.4).
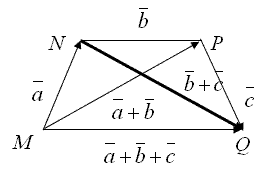
Рисунок 1.1.4
Пусть 
, 
, 
. Тогда 
, 
, 
. Следовательно,
.
Разность векторов (вычитание)
ОПРЕДЕЛЕНИЕ 1.27
Разностью векторов 
и 
называется такой вектор 
, что 
. Для построения вектора 
по данным векторам и можно воспользоваться одним из способов, сущность которых пояснена на рис. 1.1.5 и рис. 1.1.6
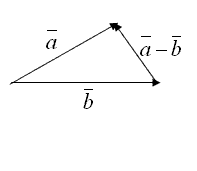
Рисунок 1.1.5
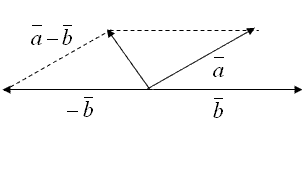
Рисунок 1.1.6
Умножение вектора на число
ОПРЕДЕЛЕНИЕ 1.28
Пусть даны вектор и число 
. Произведением вектора на число называется вектор 
, коллинеарный вектору , имеющий длину 
и то же направление, что и вектор , если 
, и противоположное направление, если 
.Если 
, то 
.
Следствие 1.
Из определения умножения вектора на число следует, что если 
, то векторы и коллинеарны. Очевидно, что если и коллинеарные векторы, то . Таким образом, два вектора и коллинеарны тогда и только тогда, когда имеет место равенство .
Следствие 2.
Противоположный вектор 
можно рассматривать как произведение вектора 
на 
, то есть 
Следствие 3.
Пусть дан вектор . Рассмотрим вектор 
, коллинеарный , направленный, как , имеющий длину, равную единице. Тогда, согласно операции умножения вектора на число, следует, что
 |
(1.33) |
Умножение вектора на число подчиняется распределительным законам
и сочетательному закону 
.
Покажем, например, справедливость первого из распределительных законов. Построим на векторах 
параллелограмм 
, на векторах 
параллелограмм 
(рис. 1.1.7). Из подобия этих параллелограммов следует, что 
.
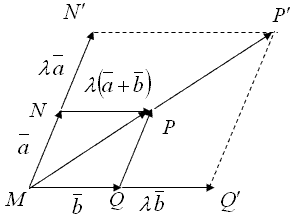
Рисунок 1.1.7
Аналогично можно убедиться и в справедливости оставшихся законов.
ПРИМЕР 1.1.17
Точка 
является центром тяжести треугольника 
. Доказать, что 
.
Решение Известно, что центр тяжести треугольника находится в точке пересечения его медиан. Обозначим через 
середину стороны 
и построим вектор 
(рис. 1.1.8).
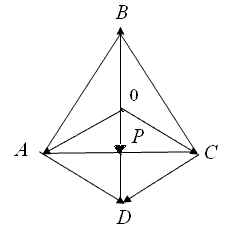
Рисунок 1.1.8
Тогда, согласно операции умножения вектора на скаляр и свойства медианы, получим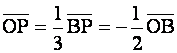 
. Построим на векторах 
и 
параллелограмм 
(рис.1.1.8).
Тогда, согласно операции сложения векторов, 
. Точка 
является точкой пересечения диагоналей этого параллелограмма.
Следовательно,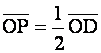 
или
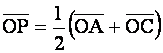. Итак,
.
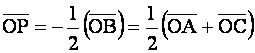Отсюда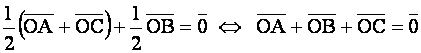 
.
