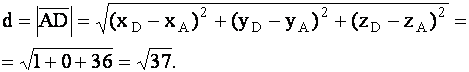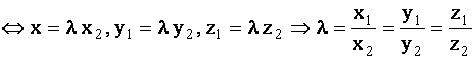Пусть векторы 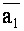 и
и 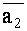 заданы в координатной форме:
заданы в координатной форме:
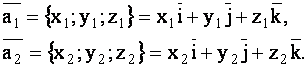 |
(1.45) |
Непосредственно из теорем 1.5 и 1.6 о проекциях векторов на ось и определения координат вектора (1.38) вытекают правила:
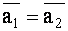 , если , если 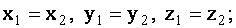 |
(1.46) |
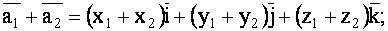 |
(1.47) |
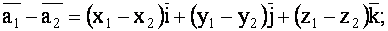 |
(1.48) |
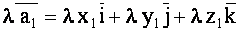 , где , где 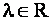 |
(1.49) |
ПРИМЕР 1.1.19
(Условие коллинеарности двух векторов).
Установить условие коллинеарности векторов 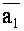 и
и 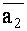 , если
, если
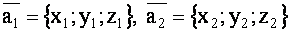 .
.
Решение Так как векторы коллинеарны, то 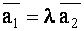 , где
, где 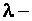 некоторое число. Согласно (1.46) — (1.49) имеем
некоторое число. Согласно (1.46) — (1.49) имеем
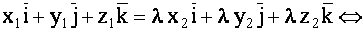
|
(1.50) |
Легко проверяется, что если координаты векторов удовлетворяют равенствам (1.50), то 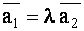
Равенства (1.50) называются условием коллинеарности двух векторов.
Координаты единичного вектора
ПРИМЕР 1.1.20
Определить координаты единичного вектора 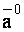 , если
, если 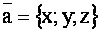 .
.
Решение.
Согласно формуле (33) 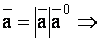
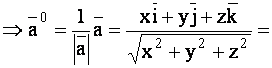
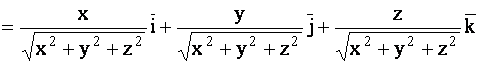 .
.
Из (1.44) следует, что
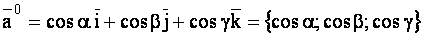 .
.
Под простейшими задачами аналитической геометрии понимаются задачи определения расстояния между двумя точками и деления некоторого отрезка в данном отношении.
Задача определения расстояния между двумя точками
Пусть в пространстве 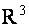 заданы своими координатами две точки
заданы своими координатами две точки 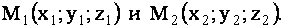 Построим векторы
Построим векторы 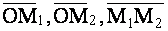 (рис. 1.1.16).
(рис. 1.1.16).
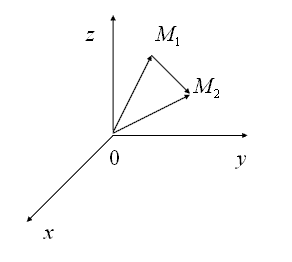
Рисунок 1.1.16
Тогда 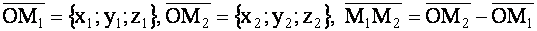
Согласно правилу (1.48)
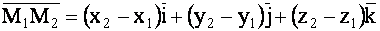 .
.
Так как длина вектора 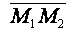 равна расстоянию между точками
равна расстоянию между точками 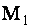 и
и 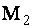 , то искомое расстояние
, то искомое расстояние 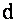 найдется по формуле (1.43). Итак,
найдется по формуле (1.43). Итак,
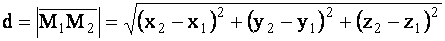 |
(1.51) |
Заметим, что в процессе решения этой задачи установлена формула определения координат вектора, если заданы координаты его начальной и конечной точек:
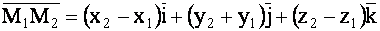 |
(1.52) |
Задача деления отрезка в данном отношении
Пусть даны две точки 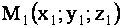 и
и 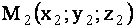 . Требуется на прямой
. Требуется на прямой 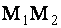 (рис. 1.1.17) найти точку
(рис. 1.1.17) найти точку 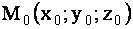 , которая разделила бы отрезок
, которая разделила бы отрезок 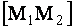 в заданном отношении
в заданном отношении 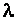 , т.е. так, что
, т.е. так, что 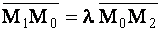 . Согласно формуле (1.52)
. Согласно формуле (1.52)
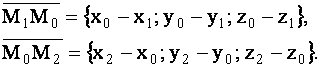
Тогда по правилу (1.49) равенство 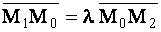 примет вид
примет вид 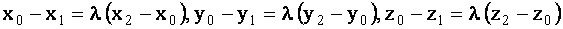 .
.
Определяя 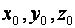 из этих равенств, получим
из этих равенств, получим
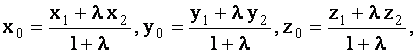 |
(1.53) |
где 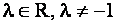 .
.
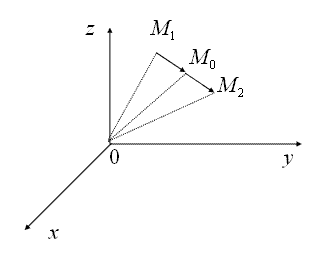
Рисунок 1.1.17
Формулы (1.53) являются формулами деления отрезка в данном отношении. В частности, при 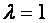 получим формулы деления отрезка пополам:
получим формулы деления отрезка пополам:
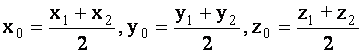 |
(1.54) |
ПРИМЕР 1.1.21
Вершины треугольника 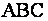 имеет координаты
имеет координаты 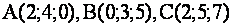 . Найти длину медианы
. Найти длину медианы 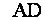 этого треугольника.
этого треугольника.
Решение Точка 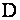 делит отрезок
делит отрезок 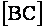 пополам. Тогда, согласно формул (1.53), получим:
пополам. Тогда, согласно формул (1.53), получим:
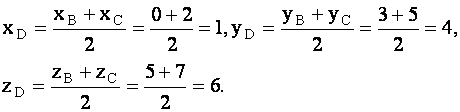
Искомое расстояние найдем по формуле (1.51)