Пусть даны два вектора 
и 
. В векторной алгебре рассматриваются два вида умножения векторов: скалярное, результатом которого является число, и векторное, результатом которого является вектор.
ОПРЕДЕЛЕНИЕ 1.34
Скалярным произведением векторов и называется число, равное произведению модулей перемножаемых векторов на косинус угла 
между ними (рис.1.1.18). Скалярное произведение обозначается символом 
. Итак,
 . |
(1.55) |
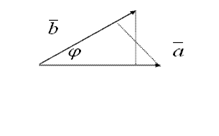
Рисунок 1.1.18
Так как 
то
 |
(1.56) |
Из (1.56) следует, что скалярное произведение векторов 
и 
равно модулю одного из векторов, умноженному на проекцию другого на направление первого вектора.
Свойства скалярного произведения векторов:
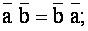
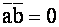, если 
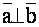или хотя бы один из векторов есть нулевой вектор (справедливо и обратное утверждение);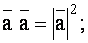
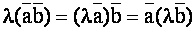для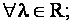 
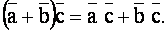
Справедливость первых четырех свойств непосредственно следует из определения скалярного произведения. Докажем справедливость распределительного свойства 5. Согласно формуле (56) и теореме 13.2 о проекции имеем
Пусть векторы и заданы своими координатами:
Найдем скалярное произведение 
. Вычислим предварительно скалярные произведения единичных векторов.
Имеем 
Векторы 
взаимно перпендикулярны. Тогда, согласно свойству 2, их произведения друг на друга равны нулю.
Используя распределительный закон скалярного произведения, получим
Итак, если векторы и заданы своими координатами, то
 . |
(1.57) |
Следствие 1.
Если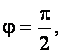 
то 
или
 . |
(1.58) |
Условие (1.58) называется условием перпендикулярности двух векторов,
Следствие 2.
Так как ,то
 |
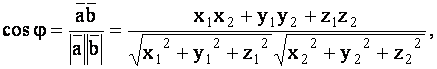(1.59) |
ПРИМЕР 1.1.22
Вычислить работу по перемещению материальной точки вдоль отрезка, из точки 
в точку 
под действием постоянной по величине и направлению силы 
Решение Из курса физики известно, что работа 
, совершаемая при указанных в примере условиях, находится по формуле 
. Так как 
, то
Ответ: 5.
ПРИМЕР 1.1.23
Даны вершины треугольника 
и 
. Определить внутренний угол треугольника при вершине 
(рис. 1.1.19)
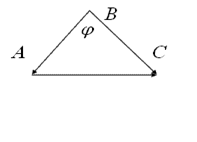
Рисунок 1.1.19
Решение Построим векторы 
и 
. Имеем
. Тогда
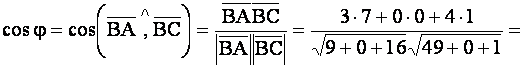
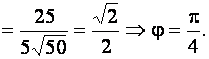
Ответ: 
Из приведенных примеров следует, что скалярное произведение векторов широко применяется в геометрии при поиске величин углов, в физике — при определении работы.
