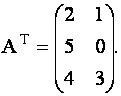Определение матрицы
Матрицей называется прямоугольная таблица, составленная из 
чисел. Для обозначения матрицы применяются круглые скобки и прописные буквы А, В, С и так далее.
Например,
 |
(1.1) |
есть общий вид записи матрицы из 
чисел.
Числа 
составляющие матрицу, называются ее элементами.
Горизонтальные ряды матрицы называются строками матрицы, вертикальные — столбцами.
Индексы 
у элемента 
, где 
означают, что этот элемент расположен в i-й строке и j-м столбце.
Например, элемент 
расположен во второй строке и в третьем столбце.
Числа 
и 
, указывающие количество строк и столбцов матрицы, называются размерами матрицы.
Наряду с обозначением (1.1) матрица обозначается также в форме:
 |
(1.2) |
,где 
Виды матриц
Матрица, у которой число строк равно числу ее столбцов называется квадратной матрицей. При этом число ее строк (столбцов) называется порядком матрицы.
Например, матрица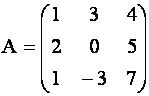 
есть квадратная матрица третьего порядка.
Квадратная матрица n-го порядка записывается в виде
 |
(1.3) |
В квадратной матрице (1.3) числа 
образуют главную диагональ матрицы, а числа 
побочную диагональ.
Квадратная матрица, у которой все числа, не стоящие на главной диагонали, равны нулю, называется диагональной матрицей.
Например, матрица 
есть диагональная матрица второго порядка.
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей. Единичную матрицу обозначают прописной буквой Е.
Например, матрица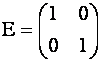 
есть единичная матрица второго порядка.
Матрица, состоящая только из одной строки, называется матрицей-строкой, состоящая только из одного столбца матрицей — столбцом.
Например, матрица А=(2 О 5 4) есть матрица — строка.
Матрица 
называется транспонированной по отношению к матрице А, если столбцы (строки) матрицы 
являются соответствующими строчками (столбцами) матрицы .
Например, если матрица равна
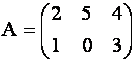, то 
