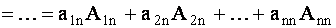Пусть дана квадратная матрица А n-го порядка
Определитель n-го порядка, соответствующий квадратной матрице А, обозначается символом
 |
(1.12) |
и определяется как число
 |
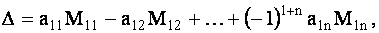(1.13) |
где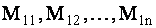 
есть миноры соответствующих элементов 
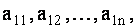, т.е. определители 
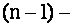го порядка, полученные из данного вычеркиванием его первой строки и соответственно первого, второго,. . . , 
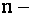го его столбцов.
Например, 
Так как каждый минор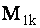 
, где 
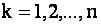есть определитель 
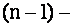го порядка, то согласно (1.13) вычисление определителя 
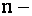го порядка сводится к вычислению 
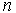определителей 
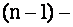го порядка.
ПРИМЕР 1.1.10
Вычислить определитель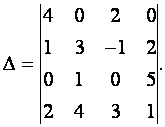 
Решение. Согласно (1.13) получим
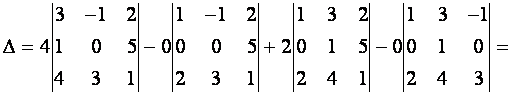
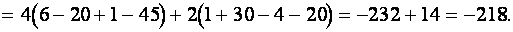
Определители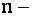 
го порядка имеют те же свойства, что и определители третьего порядка. Их справедливость проверяется с помощью соотношения (1.10).
Выберем в определителе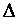 
элемент 
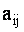, где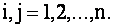 
ОПРЕДЕЛЕНИЕ 1.11 Минором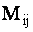 
элемента 
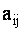определителя 
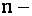го порядка называется определитель 
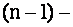го порядка, полученный из 
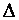вычеркиванием его 
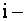й строки и 
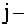го столбца.
ОПРЕДЕЛЕНИЕ 1.12 Алгебраическим дополнением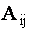 
элемента 
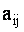называется минор 
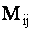этого элемента, взятый с дополнительным знаком 
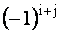, т.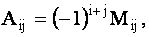е.
 где  |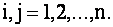
(1.14) |
Для определителей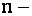 
го порядка также остается справедливой теорема разложения, т.е. определитель 
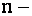го порядка равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов
|
(1.15) |
Равенство (1.15) содержат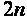 
формул, по каждой из которых можно произвести вычисление определителя.
На практике полезно перед применением теоремы разложения преобразовать определитель с помощью его свойств так, чтобы в одной из его строк (столбцов) образовалось максимальное число нулевых элементов.
ПРИМЕР 1.1.11
Вычислить определитель
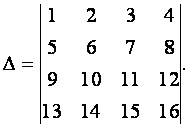
Решение. Вычитая из второго столбца первый, а из четвертого столбца третий, найдем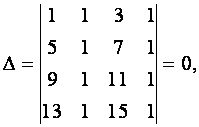 
так как образовавшийся определитель содержит два одинаковых столбца.
