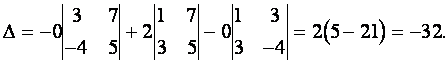Пусть дана квадратная матрица третьего порядка
ОПРЕДЕЛЕНИЕ 1.8
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
 |
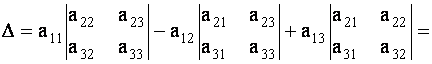(1.7) |
Определитель третьего порядка обозначается символом
 |
(1.8) |
где числа 
называются его элементами.
Индексы 
у элемента 
показывают номера строки и столбца, на пересечении которых записан этот элемент.
Например, элемент 
расположен на пересечении второй строки 
и третьего столбца 
.
Элементы 
образуют главную диагональ определителя, а элементы 
побочную диагональ.
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
ПРИМЕР 1.1.7
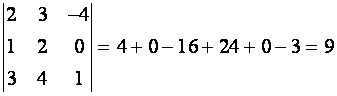
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
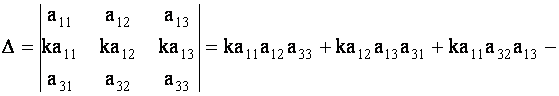
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором 
элемента , где 
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием 
й строки и 
го столбца. Так, например, минор 
элемента есть определитель
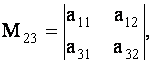а минор элемента 
есть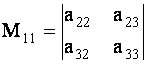 
С помощью миноров определитель (7) можно записать в виде
 |
(1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением 
элемента , где , называется минор этого элемента, взятый со знаком 
. По определению 4.3 имеем
 где / |
(1.10) |
Например,
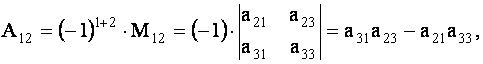
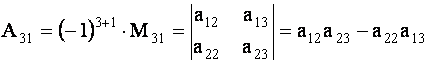и т.д.
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
|
(1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
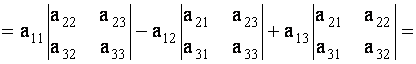
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы 
первой строки и алгебраические дополнения 
элементов второй строки определителя. Составим сумму произведений 
и покажем, что эта сумма равна нулю.
Действительно,
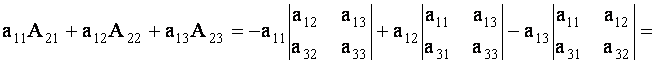
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
ПРИМЕР 1.1.8
Вычислить определитель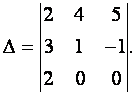 
Решение. Разложим определитель по элементам третьей строки.
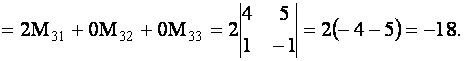
ПРИМЕР 1.1.9
Вычислить определитель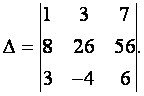 
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим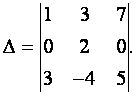 
Раскладывая этот определитель по элементам второй его строки, найдем
