Пусть даны три вектора ![]() . Так как для векторов введены два вида произведений — скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:
. Так как для векторов введены два вида произведений — скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:
1)двойное векторное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем векторное произведение полученного вектора на третий из данных векторов.
Например, вначале находится векторное произведение ![]() , затем — векторное произведение
, затем — векторное произведение ![]() ;
;
2)смешанное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем скалярное произведение полученного вектора на третий из данных векторов.
Например, вначале находится векторное произведение ![]() , затем — скалярное произведение
, затем — скалярное произведение ![]() .
.
Двойное векторное произведение обозначается в форме ![]() или в форме
или в форме ![]()
Ясно, что результатом двойного векторного произведения является вектор.
Смешанное или иначе векторно-скалярное произведение обозначается символом ![]() или символом
или символом ![]() . Результатом смешанного произведения является число.
. Результатом смешанного произведения является число.
Пусть требуется определить смешанное произведение векторов, если известны координаты этих векторов
![]() .
.
Вычислим предварительно ![]() Имеем
Имеем

Воспользовавшись формулой (1.57), найдем
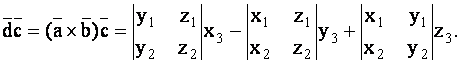
Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме
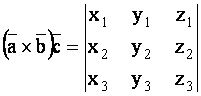 |
(1.62) |
Формула (1.62) дает выражение для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов ![]() записаны соответственно в первой, второй и третьей строках определителя.
записаны соответственно в первой, второй и третьей строках определителя.
Покажем, что для смешанного произведения векторов справедливы равенства
| (1.63) |
Проверим, например, справедливость равенства ![]() Согласно формуле (1.62) имеем
Согласно формуле (1.62) имеем
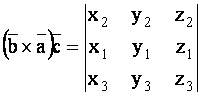
Как известно, при перестановке двух срок определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на ![]() , получим
, получим

Итак, ![]()
Формулы (1.63) проще всего запомнить с помощью правила круговой перестановки векторов, сущность которого пояснена на рис.1.1.25 и 1.1.26.
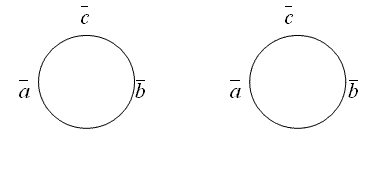
Рисунки 1.1.25 и 1.1.26
Выясним геометрический смысл смешанного произведения векторов ![]() . Отложим векторы
. Отложим векторы ![]() от общего начала и построим на этих векторах, как на ребрах, параллелепипед (рис.1.1.27).
от общего начала и построим на этих векторах, как на ребрах, параллелепипед (рис.1.1.27).
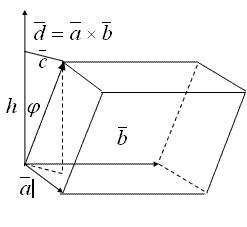
Рисунок 1.1.27
Пусть ![]() . Тогда, согласно определения векторного произведения векторов, модуль вектора
. Тогда, согласно определения векторного произведения векторов, модуль вектора ![]() равен площади
равен площади ![]() параллелограмма, построенного на векторах
параллелограмма, построенного на векторах ![]() как на сторонах. Следовательно,
как на сторонах. Следовательно,
![]() где
где 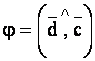
Обозначим через ![]() высоту параллелепипеда, опущенную из конца вектора
высоту параллелепипеда, опущенную из конца вектора ![]() на рассматриваемый параллелограмм, и выясним смысл произведения
на рассматриваемый параллелограмм, и выясним смысл произведения ![]() . Вектор
. Вектор ![]() перпендикулярен плоскости параллелограмма, тогда
перпендикулярен плоскости параллелограмма, тогда
![]() если
если 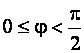 и
и
![]() , если
, если 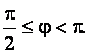
Следовательно, если ![]() есть объем параллелепипеда, то
есть объем параллелепипеда, то
![]() , если
, если 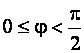 и
и
![]() ,если
,если 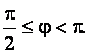
Итак,
| (1.64) |
Равенство (1.64) означает, что модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах как на ребрах.
Следствие (условие компланарности трех векторов). Для того, чтобы три вектора ![]() были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т.е.
были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т.е. ![]() или в координатной форме
или в координатной форме
 |
(1.65) |
Необходимость Пусть векторы ![]() компланарны. Тогда вектор
компланарны. Тогда вектор ![]() перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору
перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору ![]() . Поэтому
. Поэтому
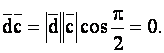 Следовательно,
Следовательно, ![]()
Достаточность Пусть векторы ![]() таковы, что
таковы, что ![]()
Если предположить, что векторы не компланарны, то на них можно построить параллелепипед с объемом ![]() . Но, согласно формуле (64)
. Но, согласно формуле (64)
![]() Следовательно,
Следовательно, ![]() или,
или, ![]() , что противоречит исходному утверждению.
, что противоречит исходному утверждению.
ПРИМЕР 1.1.26
Вычислить объем треугольной пирамиды с вершинами в точках ![]()
Решение. Построим три вектора
![]() с общим началом точкой
с общим началом точкой ![]() . На этих векторах, как на ребрах, построим параллелепипед. Его объем равен
. На этих векторах, как на ребрах, построим параллелепипед. Его объем равен ![]() Объем пирамиды
Объем пирамиды ![]() составляет шестую долю объема параллелепипеда. Следовательно,
составляет шестую долю объема параллелепипеда. Следовательно,
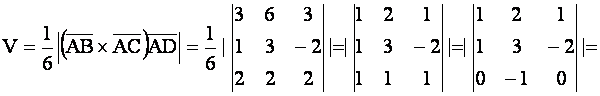
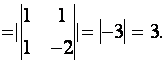 Ответ: 3
Ответ: 3
Из геометрического смысла смешанного произведения векторов и рассмотренного примера следует, что оно широко используется при вычислении объемов любых многогранников.